Asimtot datar dan Tegak Fungsi Rasional Bagian I

Pada postinagn kali ini saya akan menjelaskan bagaimana mencari asimtot tegak dan datar pada fungsi rasional secara mudah. Seperti kita ketahui pada soal TKDST SBMPTN 2017 salah satu soalnya menyinggung tentang asimtot tegak dan datar.

Pengertian asimtot
Asimtot adalah suatu garis lurus yang didekati oleh kurva lengkung dengan jarak semakin lama semakin kecil mendekati nol di jauh tak terhingga. Asimtot juga bisa diartikan dengan sebuah garis lurus yang sangat dekat dengan kurva lengkung di titik jauh tak terhingga.

Macam - macam asimtot
yaitu asimtot datar, asimtot tegak dan asimtot miring. Asimtot datar adalah garis tersebut sejajar dengan sumbu x. asimtot tegak adalah garis tersebut sejajar dengan sumbu y. dan asimtot miring adalah garis tersebut tidak sejajar dengan sumbu x dan dengan sumbu y.

Fungsi yang mempunyai asimtot
Fungsi yang memiliki asimtot adalah fungsi rasional. Tepatnya lagi adalah fungsi yang memiliki asimtot adalah fungsi rasional pecahan. Fungsi rasional pecahan terbagi menjadi sangat banyak macamya.. misalnya saja beberapa macamnya yaitu : pembilang dan penyebut keduanya adalah fungsi linear. Ada juga yang pembilang dan penyebutnya merupakan fungsi kuadrat. Ada yang berbeda antara pembilang dan penyebut. Pembilang fungsi linear dan penyebut fungsi kuadrat. Atau sebaliknya…

Fungsi rasional dengan pembilang dan penyebut keduanya adalah fungsi linear



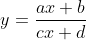
Asimtot Tegak
untuk memperoleh asimtot tegak maka menggunakan limit y menuju tak hingga






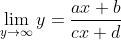
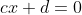
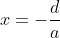
∴ asimtot tegaknya adalah
  

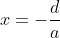
Asimtot Datar
untuk memperoleh asimtot datar maka menggunakan limit x menuju tak hingga




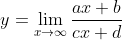
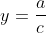
Contoh :
Tentukan asimtot tegak dan datar



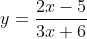
asimtot tegak :
3x + 6 = 0
3x = - 6
x = - 2
∴ asimtot tegaknya adalah x = - 2

asimtot datar :

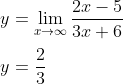
∴ asimtot datarnya adalah
 
Latihan 
Tentukan asimtot datar dan tegak fungsi rasional di bawah ini


Jawaban 
Lihat DISINI

Posted in: asimtot,fungsi rasional