Pada postingan kali ini saya akan membahas soal-soal simak ui matematika dasar tahun 2011 kode 212. Pembahasan soal ini tidak sekaligus dalam waktu yang sama. Jadi tetaplah berkunjung ke blog ini untuk mendapatkan sesuatu yang baru. Semoga dengan pembahasan ini bisa membantu dalam persiapan masuk ui jalur SNMPTN maupun SIMAK.

dengan
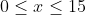
---------------------------------------------------------------------------------
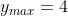
apabila
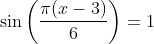

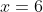
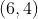
----------------------------------------------------------------------------------
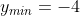
apabila
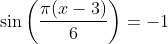
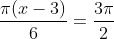
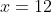
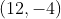
-----------------------------------------------------------------------------------
jarak titik (6,4) dan (12,-4) adalah
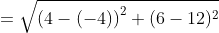
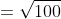
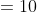
----------------------------------------------------------------------------------
2.C (Suku Banyak)
Diketahui
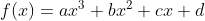
adalah polinomial dengan derajat tiga yang memenuhi persamaan berikut:
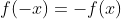
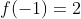
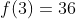
maka
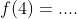
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
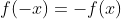
berarti f(x) fungsi ganjil, sehingga
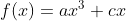
----------------------------------------------------------------------------------
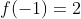
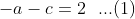
----------------------------------------------------------------------------------
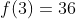
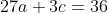
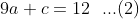
----------------------------------------------------------------------------------
eliminasi persamaan (1) dan (2) diperoleh
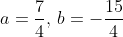
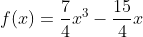
----------------------------------------------------------------------------------
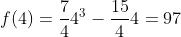
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
perhatikan gambar di atas !
Karena garis g sejajar gris singgung h berarti
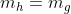
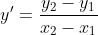
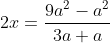
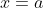
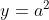
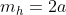
persamaan garis singgung di titik
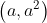
bergradien 2a adalah...
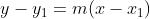
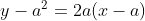
memotong sumbu y berarti x = 0 sehingga diperoleh
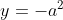
----------------------------------------------------------------------------------
Huruf-huruf A,H,I,M,O,T,U,V,W,X,Z akan terlihat sama jika dilihat melalui sebuah kaca. Huruf-huruf ini di namakan huruf simetri. Berapa banyaa cara untuk memilih kata sandi yang terdiri dari 3 huruf dengan paling sedikit 2 huruf simetri?
----------------------------------------------------------------------------------
Diketahui definisi dari IxI adalah bilangan bulat terbesar yang lebih kecil atau sama dengan x.Sebagai contoh I5I = 5; I2,9I=2; I-2,5I = -3.Jika y adalah bilangan riil yang bukan merupakan bilangan bulat, maka IyI+I2-yI adalah ....
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
Perhatikan gambar !
terlihat pada gambar nilai I 2 - y I = 1 - I y I
sehingga I y I + I 2 - y I = I y I + 1 - I y I = 1
-----------------------------------------------------------------
6. A (Trigonometri)
Jika
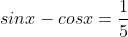
jumlah dari semua nilai tan x yang memenuhi adalah....
---------------------------------------------------------------------------------
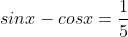
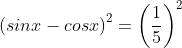
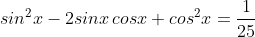
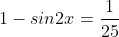
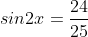
-----------------------------------------------------------
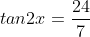
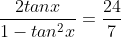
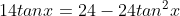
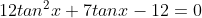
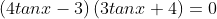
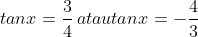
----------------------------------------------------------
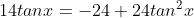
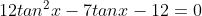
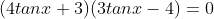
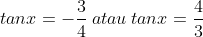
Jumlah semua tan x = 0
Jika x adalah sudut lancip,maka jumlah semua nilai x yang memenuhi persamaan
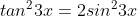
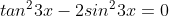
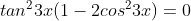
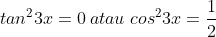
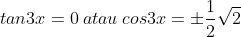
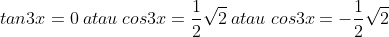
karena x lancip maka yang memenuhi adalah
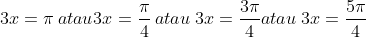
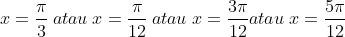
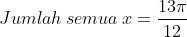
----------------------------------------------------------------------------------
1. E (Trigonometri)
Jarak antara titik maksimum dan minimum pada kurva dari fungsidengan
---------------------------------------------------------------------------------
Jawab
--------------------------------------------------------------------------------- apabila
----------------------------------------------------------------------------------
apabila
-----------------------------------------------------------------------------------
jarak titik (6,4) dan (12,-4) adalah
----------------------------------------------------------------------------------
2.C (Suku Banyak)
adalah polinomial dengan derajat tiga yang memenuhi persamaan berikut:
maka
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
berarti f(x) fungsi ganjil, sehingga
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
eliminasi persamaan (1) dan (2) diperoleh
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
3. A (Fungsi Kuadrat)
Dua titik dengan x1 = -a dan x2 = 3a dimana a tidak sama dengan nol, terletak pada parabola y = x^2. Garis g menghubungkan kedua titik tersebut. Jika garis singgung parabola di suatu titik sejajar dengan garis g, maka garis singgung tersebut akan memotong sumbu y di ....----------------------------------------------------------------------------------
Jawab :
----------------------------------------------------------------------------------perhatikan gambar di atas !
Karena garis g sejajar gris singgung h berarti
persamaan garis singgung di titik
bergradien 2a adalah...
memotong sumbu y berarti x = 0 sehingga diperoleh
----------------------------------------------------------------------------------
4. C (Peluang)
Huruf-huruf A,H,I,M,O,T,U,V,W,X,Z akan terlihat sama jika dilihat melalui sebuah kaca. Huruf-huruf ini di namakan huruf simetri. Berapa banyaa cara untuk memilih kata sandi yang terdiri dari 3 huruf dengan paling sedikit 2 huruf simetri?
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
Ada : 26 huruf ( 11 simetri dan 15 tidak)
Ambil : 3 huruf ( paling sedikit 2 huruf simetri)
----------------------------------------------------------------------------------
Ada dua kemungkinan : (asumsikan tidak ada huruf yang sama)
----------------------------------------------------------------------------------
Pertama : 2 simetri 1 tidak
Posisi yang tidak di belakang : 11.10.15 =1650
Posisi yang tidak di depan : 15.11.10 =1650
Posisi yang tidak di tengah : 11.15.10 = 1650
----------------------------------------------------------------------------------
Posisi yang tidak di depan : 15.11.10 =1650
Posisi yang tidak di tengah : 11.15.10 = 1650
----------------------------------------------------------------------------------
Kedua : 3 simetri
11.10.9 = 990
----------------------------------------------------------------------------------
jumlah seluruhnya 1650.3 + 990 = 5940----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
5. C (Bilangan Bulat)
Diketahui definisi dari IxI adalah bilangan bulat terbesar yang lebih kecil atau sama dengan x.Sebagai contoh I5I = 5; I2,9I=2; I-2,5I = -3.Jika y adalah bilangan riil yang bukan merupakan bilangan bulat, maka IyI+I2-yI adalah ....
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
Perhatikan gambar !
terlihat pada gambar nilai I 2 - y I = 1 - I y I
sehingga I y I + I 2 - y I = I y I + 1 - I y I = 1
-----------------------------------------------------------------
6. A (Trigonometri)
Jika
jumlah dari semua nilai tan x yang memenuhi adalah....
---------------------------------------------------------------------------------
Jawab
---------------------------------------------------------------------------------------------------------------------------------------------
kasus pertama :
----------------------------------------------------------- ----------------------------------------------------------
kasus kedua :
----------------------------------------------------------
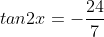
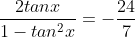
Jumlah semua tan x = 0
--------------------------------------------------------------------
7. B (Trigonometri)
7. B (Trigonometri)
Jika x adalah sudut lancip,maka jumlah semua nilai x yang memenuhi persamaan
karena x lancip maka yang memenuhi adalah
----------------------------------------------------------------------------------
9.D/E (Sistem Persamaan)
x,y,z tidak nol dan bilangan bulat positif
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------eliminasi pers (1) dan (2) di peroleh
z = 2010 atau z = 2011
10. A(Trigonometri)
Diketahui bahwa cos (2A - B) + sin (A + B) = 2 dan b = 2V3,
maka a = ...
Jawab
cos (2A - B) + sin (A + B) = 2
cos (2A - B) = 1 dan sin (A + B) = 1
2A - B = 0 ...(1)
A + B = 90 ...(2)
di eliminasi dan substitusi
A = 30, B = 60 sehingga C = 90
a : sin A = b : sin B
a : sin 30 = 2V3 : sin 60
a : 0,5 = 2V3 : 0,5 V3
a = 2
11.B ( Turunan )
Soal
Jawab :
3x - 6 = 3 atau 3x - 6 = - 3
x = 3 atau x = 1
substitusi ke garis atau kurva, di peroleh :
y = 5 atau y = - 7/3
(3,5) = (a,b) atau (1, -7/3) = (a,b)
syarat : a < b
a - b = 3 - 5 = - 2
12.E(Persamaan Kuadrat)
Soal
Jawab :
4a + 10 - 12 = 0
a = 1/2
13.D (Pertidaksamaan)
Soal
Jawab :
Syarat akar :
(1) dan (2) di iris
14.C (Logaritma)
Soal
Jawab :
15.A (Fuungsi Kuadrat)
Soal
Jawab :
a, b, c > 0
teori kesebangunan
dari (1) dan (2) diperoleh
16. tak terhingga (Program linier)
Soal
Jawab :
agar daerahnya berbentuk segitiga maka
garis 4x + 5y = c terletak diantara
garis 4x + 5y = 0 dan garis 4x + 5y = 15
jadi c bisa di tulis :
atau
sehingga banyaknya bilangan bulat c tidak terhingga,
17.A (Turunan)
Soal
Jawab :
ada
di eliminasi di peroleh :
f(2) = 2, dan g(2) = 1
18.A (Statistik)
Soal
Jawab :
misalkan anak termuda : x
berturut - turut dari yang termuda adalah :
x, 2x - 3, x + 4, 2x - 5, 2x
* rata - rata = 16
x = 5
kuadrat dari selisih umur anak kedua dan anak ketiga adalah :
19.4 (Matriks)
Soal
Jawab :
*
20.C (Persamaan Kuadrat)
Soal
Jawab :
substitusikan (1) dan (2) ke (3) di peroleh
karena 2011 bilangan prima berarti
atau
perhatian !
pembahasan ini tidak mewakili instansi manapun























5 komentar:
pak saya salah satu siswa bimbel di nurul fikri,, kalau boleh tawu disub menu bagian mana ada pembahasan T.O matematika yang bapak bilang kemarin
terima kasih pak, di tunggu jawabannya
Pembahasanya ada di posting dengan judul program superintensif snmptn 2012. silahkan lihat dan unduh
assalamualaikum,pak kok pembahasan soalnya gak sampe nomer 20 ya pak?hehe
belum sempat karena sibuk dengan pekerjaan. mohon maaf ya..hehehe..
kode simak ui 2012
kemampuan dasar 224, 325, 326, 327
kemampuan ipa 521, 522, 523, 524
Post a Comment