Update : Rabu, 28/08/2019
Table Of Content
A. Pengertian
A.1.Bentuk Umum :
A.2.Nilai Diskriminan
A.3.Soal dan Bahas
A.4.Video
B. Menyelesaikan Persamaan dan Pertidaksamaan Kuadrat
B.1.Menyelesaikan Persamaan Kuadrat
B.1.1.Pemfaktoran
B.1.2.Kuadrat Sempurna
B.1.3.Rumus ABC/Al Khawarizmi
B.2.Menyelesaikan Pertidaksamaan Kuadrat
C. Jenis-jenis Akar Persamaan Kuadrat
C.1. Akar Real
C.1.1.Akar Real Berbeda
C.1.2.Akar Real Sama
C.2. Akar Imajiner
C.1. Akar Real
C.1.1.Akar Real Berbeda
C.1.2.Akar Real Sama
C.2. Akar Imajiner
D. Operasi Akar Persamaan Kuadrat
D.1.Dasar
D.2.Lanjutan
D.1.Dasar
D.2.Lanjutan
E. Hubungan Dua Akar Persamaan Kuadrat
E.1. Dua Akar Real Positif
E.1. Dua Akar Real Positif
F. Menyusun Persamaan Kuadrat
G. Akar-akar Persekutuan Dua Persamaan Kuadrat
Persamaan Kuadrat Satu Variabel (Persamaan Kuadrat)
A. Pengertian
Persamaan Kuadrat Satu Variabel atau sering disebut persamaan kuadrat adalah kalimat terbuka yang menyatakan hubungan sama dengan dan memiliki satu variabel yang salah satu variabelnya berpangkat dua.A.1.Bentuk Umum :
Persamaan Kuadrat dalam bentuk umumnya ditulis sebagaidengan x variabel dan a,b,c konstanta
Nilai x yang memenuhi persamaan kuadrat disebut himpunan penyelesaian atau sering disebut sebagai akar-akar persamaan kuadrat.
A.2.Diskriminan (D) :
Diskriminan persamaan kuadrat disimbolkan dengan D, adalah nilai tertentu suatu persamaan kuadrat yang memenuhi D = b^2 - 4ac. Diskriminan ini dipakai untuk menentukan jenis akar dan nilai akar dengan rumus abc (rumus Al -Khawarizmi)A.3.Soal 1
Berdasarkan bentuk umum persamaan kuadrat ax^2 + bx + c = 0, tentukanlah nilai a,b, c dan D dari persamaan kuadrat berikut ini
1. x^2 - x + 4 = 0 ⇾ a =1
b =-1
c =4
D =(-1)^2-41.4=1-16=-15
2. -2x^2 + 3x - 5 = 0 ⇾ a =-2
b =3
c =-5
D =3^2-4.(-2)(-5)=9-40=-31
3. px^2 - (p + 1)x - (p - 2) = 0 ⇾ a =p
b =-(p+1)=-p-1
c =-(p-2)=-p+2
D =(-p-1)^2-4.p.(-p+2)=p^2+2p+1+4p^2-8p=5p^2-6p+1
A.4.lihat video di sini
B. Menyelesaikan Persamaan dan Pertidaksamaan Kuadrat
B.1.Menyelesaikan Persamaan Kuadrat
Menyelesaikan Persamaan Kuadrat adalah mencari nilai x yang memenuhi persamaan kuadrat atau mencari nilai akar-akar persamaan kuadrat tersebut
Untuk menyelesaikan persamaan kuadrat dapat dilakukan dengan tiga cara, yaitu :
1. Pemfaktoran atau memfaktorkan
Cara ini dapat dilakukan apabila nilai diskriminan adalah bilangan kuadrat (D = p^2)
Dari bentuk umum persamaan kuadrat dirubah menjadi bentuk faktornya, yaitu :
ax^2 + bx + c = 0
(x - m)(x - n) = 0
x - m = 0 atau x - n = 0
x = m atau x = n
Contoh dibawah ini adalah contoh dengan nilai a = 1:
1. x^2 - 1x - 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Selisih (karena tanda c negatif, jadi selisih ) dua bilangan hasilnya
angka 1 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
3x2
sebab 3 - 2 = 1
dapat ditulis sebagai berikut
(x 3)(x 2) = 0
selanjutnya menentukan tanda positif atau negatif angka 3 dan
angka 2. Dari angka dua dan tiga, angka yang paling besar adalah
angka 3, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 3)(x 2) = 0
selanjutnya untuk menentukan tanda angka dua, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (negatif) bentuk umum,
dengan hasil positif
(x - 3)(x + 2) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 3 = 0 atau x + 2 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 3 atau x = - 2
selanjutnya angaka 3 atau - 2 disebut sebagai akar-akar persamaan
kuadrat x^2 - x - 6 = 0
2. x^2 - 5x - 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Selisih (karena tanda c negatif, jadi selisih ) dua bilangan hasilnya
angka 5 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
6x1
sebab 6 - 1 = 5
dapat ditulis sebagai berikut
(x 6)(x 1) = 0
selanjutnya menentukan tanda positif atau negatif angka 6 dan
angka 1. Dari angka enam dan satu, angka yang paling besar adalah
angka 6, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 6)(x 1) = 0
selanjutnya untuk menentukan tanda angka satu, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (negatif) bentuk umum,
dengan hasil positif
(x - 6)(x + 1) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 6 = 0 atau x + 1 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 6 atau x = - 1
selanjutnya angaka 6 atau - 1 disebut sebagai akar-akar persamaan
kuadrat x^2 - 5x - 6 = 0
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Jumlah (karena tanda c positif, jadi jumlah ) dua bilangan hasilnya
angka 5 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
3x2
sebab 3 + 2 = 5
dapat ditulis sebagai berikut
(x 3)(x 2) = 0
selanjutnya menentukan tanda positif atau negatif angka 3 dan
angka 2. Dari angka tiga dan dua, angka yang paling besar adalah
angka 3, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 3)(x 2) = 0
selanjutnya untuk menentukan tanda angka dua, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (positif) bentuk umum,
dengan hasil negatif
(x - 3)(x - 2) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 3 = 0 atau x - 2 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 3 atau x = 2
selanjutnya angaka 3 atau 2 disebut sebagai akar-akar persamaan
kuadrat x^2 - 5x + 6 = 0
4. x^2 + 7x + 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Jumlah (karena tanda c positif, jadi jumlah ) dua bilangan hasilnya
angka 7 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
6x1
sebab 6 + 1 = 7
dapat ditulis sebagai berikut
(x 6)(x 1) = 0
selanjutnya menentukan tanda positif atau negatif angka 6 dan
angka 1. Dari angka 6 dan 1, angka yang paling besar adalah
angka 6, tanda pada angka yang paling besar mengikuti
tanda "b" bentuk umum, yaitu positif
(x + 6)(x 1) = 0
selanjutnya untuk menentukan tanda angka 1, yaitu dengan cara
kalikan tanda b (positif) dengan tanda c (positif) bentuk umum,
dengan hasil positif
(x + 6)(x + 1) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x + 6 = 0 atau x + 1 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = - 6 atau x = - 1
selanjutnya angaka - 6 atau - 1 disebut sebagai akar-akar persamaan
kuadrat x^2 + 7x + 6 = 0
Lihat Video Pemfaktoran klik di sini
Latihan :
1. x^2 - 2x - 24 = 0
2. x^2 - 10x + 24 = 0
3. x^2 - 5x - 24 = 0
4. x^2 - 11x + 24 = 0
5. x^2 + 25x + 24 = 0
Dari bentuk umum persamaan kuadrat dirubah menjadi bentuk faktornya, yaitu :
ax^2 + bx + c = 0
(x - m)(x - n) = 0
x - m = 0 atau x - n = 0
x = m atau x = n
Contoh dibawah ini adalah contoh dengan nilai a = 1:
1. x^2 - 1x - 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Selisih (karena tanda c negatif, jadi selisih ) dua bilangan hasilnya
angka 1 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
3x2
sebab 3 - 2 = 1
dapat ditulis sebagai berikut
(x 3)(x 2) = 0
selanjutnya menentukan tanda positif atau negatif angka 3 dan
angka 2. Dari angka dua dan tiga, angka yang paling besar adalah
angka 3, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 3)(x 2) = 0
selanjutnya untuk menentukan tanda angka dua, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (negatif) bentuk umum,
dengan hasil positif
(x - 3)(x + 2) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 3 = 0 atau x + 2 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 3 atau x = - 2
selanjutnya angaka 3 atau - 2 disebut sebagai akar-akar persamaan
kuadrat x^2 - x - 6 = 0
2. x^2 - 5x - 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Selisih (karena tanda c negatif, jadi selisih ) dua bilangan hasilnya
angka 5 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
6x1
sebab 6 - 1 = 5
dapat ditulis sebagai berikut
(x 6)(x 1) = 0
selanjutnya menentukan tanda positif atau negatif angka 6 dan
angka 1. Dari angka enam dan satu, angka yang paling besar adalah
angka 6, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 6)(x 1) = 0
selanjutnya untuk menentukan tanda angka satu, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (negatif) bentuk umum,
dengan hasil positif
(x - 6)(x + 1) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 6 = 0 atau x + 1 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 6 atau x = - 1
selanjutnya angaka 6 atau - 1 disebut sebagai akar-akar persamaan
kuadrat x^2 - 5x - 6 = 0
3. x^2 - 5x + 6 = 0
Jawab :Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Jumlah (karena tanda c positif, jadi jumlah ) dua bilangan hasilnya
angka 5 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
3x2
sebab 3 + 2 = 5
dapat ditulis sebagai berikut
(x 3)(x 2) = 0
selanjutnya menentukan tanda positif atau negatif angka 3 dan
angka 2. Dari angka tiga dan dua, angka yang paling besar adalah
angka 3, tanda pada angka yang paling besar mengikuti tanda "b"
bentuk umum, yaitu negatif
(x - 3)(x 2) = 0
selanjutnya untuk menentukan tanda angka dua, yaitu dengan cara
kalikan tanda b (negatif) dengan tanda c (positif) bentuk umum,
dengan hasil negatif
(x - 3)(x - 2) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x - 3 = 0 atau x - 2 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = 3 atau x = 2
selanjutnya angaka 3 atau 2 disebut sebagai akar-akar persamaan
kuadrat x^2 - 5x + 6 = 0
4. x^2 + 7x + 6 = 0
Jawab :
Perkalian dua bilangan menghasilkan angka 6 :
6x1
3x2
Jumlah (karena tanda c positif, jadi jumlah ) dua bilangan hasilnya
angka 7 (angka warna biru), dari dua pilihan diatas yang
dipilih adalah
6x1
sebab 6 + 1 = 7
dapat ditulis sebagai berikut
(x 6)(x 1) = 0
selanjutnya menentukan tanda positif atau negatif angka 6 dan
angka 1. Dari angka 6 dan 1, angka yang paling besar adalah
angka 6, tanda pada angka yang paling besar mengikuti
tanda "b" bentuk umum, yaitu positif
(x + 6)(x 1) = 0
selanjutnya untuk menentukan tanda angka 1, yaitu dengan cara
kalikan tanda b (positif) dengan tanda c (positif) bentuk umum,
dengan hasil positif
(x + 6)(x + 1) = 0
selanjutnya, dua angka jika dikalikan hasilnya nol berarti angka pertama
sama dengan nol atau angka kedua sama dengan nol, dpt ditulis sebagai
berikut
x + 6 = 0 atau x + 1 = 0
selanjutnya, angka dipindah keruas kanan, dapat ditulis sebagi berikut
x = - 6 atau x = - 1
selanjutnya angaka - 6 atau - 1 disebut sebagai akar-akar persamaan
kuadrat x^2 + 7x + 6 = 0
Lihat Video Pemfaktoran klik di sini
Latihan :
1. x^2 - 2x - 24 = 0
2. x^2 - 10x + 24 = 0
3. x^2 - 5x - 24 = 0
4. x^2 - 11x + 24 = 0
5. x^2 + 25x + 24 = 0
2. Melengkapkan Kuadrat Sempurna
Cara ini dapat dilakukan dengan mengubah bentuk umum persamaan kuadrat
ax^2 + bx + c = 0 menjadi bentuk kuadrat sempurna a(x - p)^2 = q
Dari bentuk umum persamaan kuadrat dengan a = 1 dirubah menjadi bentuk
kuadrat sempurna, langkah-langkahnya yaitu :
x^2 + bx + c = 0
x^2 + bx = - c
x^2 + bx + (b/2)^2 = - c + (b/2)^2
(x + b/2)^2 = -c + (b/2)^2
x + b/2 = (-c + (b^2/4)) atau x + b/2 = -(-c + (b^2/4))
x = -b/2 + (-c + (b^2/4)) atau x = -b/2 - (-c + (b^2/4))
Contoh
1. x^2 - x - 6 = 0
Jawab
x^2 - x = 6
x^2 - x + (1/2)^2 = 6 + (1/2)^2
x^2 - x + 1/4 = 6 + 1/4
(x - 1/2)^2 = 25/4
x - 1/2 = +5/2 atau x - 1/2 = -5/2
x = 1/2 + 5/2 atau x = 1/2 - 5/2
x = 6/2 atau x = -4/2
x = 3 atau x = -2
2. x^2 - 2x - 24 = 0
Jawab
x^2 - 2x = 24
x^2 - 2x + (2/2)^2 = 24 + (2/2)^2
x^2 - 2x + 1 = 24 + 1
(x - 1)^2 = 25
x - 1 = 5 atau x - 1 = -5
x = 6 atau x = -4
Latihan
1. x^2 - 4x - 12 = 0
Dari bentuk umum persamaan kuadrat dengan a = 1 dirubah menjadi bentuk
kuadrat sempurna, langkah-langkahnya yaitu :
x^2 + bx + c = 0
x^2 + bx = - c
x^2 + bx + (b/2)^2 = - c + (b/2)^2
(x + b/2)^2 = -c + (b/2)^2
x + b/2 = (-c + (b^2/4)) atau x + b/2 = -(-c + (b^2/4))
x = -b/2 + (-c + (b^2/4)) atau x = -b/2 - (-c + (b^2/4))
Contoh
1. x^2 - x - 6 = 0
Jawab
x^2 - x = 6
x^2 - x + (1/2)^2 = 6 + (1/2)^2
x^2 - x + 1/4 = 6 + 1/4
(x - 1/2)^2 = 25/4
x - 1/2 = +5/2 atau x - 1/2 = -5/2
x = 1/2 + 5/2 atau x = 1/2 - 5/2
x = 6/2 atau x = -4/2
x = 3 atau x = -2
2. x^2 - 2x - 24 = 0
Jawab
x^2 - 2x = 24
x^2 - 2x + (2/2)^2 = 24 + (2/2)^2
x^2 - 2x + 1 = 24 + 1
(x - 1)^2 = 25
x - 1 = 5 atau x - 1 = -5
x = 6 atau x = -4
Latihan
1. x^2 - 4x - 12 = 0
2. x^2 - 10x + 24 = 0
3. x^2 + 6x + 8 = 0
3. Rumus abc atau rumus Al-Khawarizmi3. x^2 + 6x + 8 = 0
Cara ini dapat dilakukan dengan mencari nilai a,b, dan c kemudian
nilai akar-akarnya (x1, x2) dapat di cari dengan rumus :
Menyelesaikan pertidaksamaan kuadrat adalah menentukan interval nilai x yang memenuhi pertidaksamaan kuadrat
Langkah-langkah menyelsaikan Pertidaksamaan Kuadrat adalah, sebagi berikut :
1. Tentukan akar-akar persamaan kuadrat. Nilai akar-akar ini sebagai batas-batas interval
2. Buat garis bilangan, tentukan tanda positif atau negatif untuk setiap interval x pada garis bilangan
3. Pilih interval x yang bertanda sama dengan pertidaksmaan
C. Jenis-jenis Akar Persamaan Kuadrat
Suatu persamaan kuadrat dapat diketahui jenis akarnya tanpa perlu menentukan akar-akarnya dengan cara melihat nilai diskriminan persamaan kuadrat tersebut. Berikut adalah jenis-jenis akar dilihat dari nilai diskriminan
a. Akar real (Nyata)
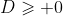
a.1. berbeda
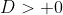
a.2. sama
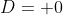
b. Akar imajiner (Khayal)
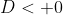
lihat video di sini
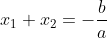
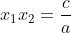
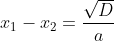
b. rumus turunannya
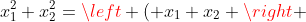%5E%7B2%7D-2x_%7B1%7Dx_%7B2%7D)
%5E%7B3%7D-3x_%7B1%7Dx_%7B2%7D%5Cleft+(+x_%7B1%7D+x_%7B2%7D+%5Cright+))
%5E%7B2%7D-2x_%7B1%7Dx_%7B2%7D+%5Cright+%5C%7D%5E%7B2%7D-2%5Cleft+%5C%7B+x_%7B1%7Dx_%7B2%7D+%5Cright+%5C%7D%5E%7B2%7D)
%5Cleft+(+x_%7B1%7D+x_%7B2%7D+%5Cright+))
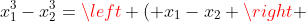%5E%7B3%7D+2x_%7B1%7Dx_%7B2%7D%5Cleft+(+x_%7B1%7D-x_%7B2%7D+%5Cright+))
lihat video klik di sini
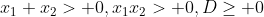
b. dua akar negatif
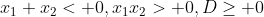
c. dua akar berlainan tanda
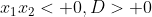
d. dua akar berlawanan
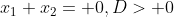
e. dua akar berkebalikan
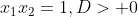
lihat video di sini
x+(perkalian%5C,+akar)=0)
lihat video 1 di sini
lihat video 2 di sini
a. Akar real (Nyata)
a.1. berbeda
a.2. sama
b. Akar imajiner (Khayal)
lihat video di sini
D. Operasi Akar Persamaan Kuadrat
a. rumus dasarb. rumus turunannya
lihat video klik di sini
E. Hubungan Dua Akar Persamaan Kuadrat
a. dua akar positifb. dua akar negatif
c. dua akar berlainan tanda
d. dua akar berlawanan
e. dua akar berkebalikan
lihat video di sini
F. Menyusun Persamaan Kuadrat
lihat video 1 di sini
lihat video 2 di sini
G. Akar-akar Persekutuan Dua Persamaan Kuadrat
a. memiliki satu akar persekutuan
eliminasikan
b. memiliki dua akar persekutuan


















0 komentar:
Post a Comment