Pada postingan kali ini saya akan membahas soal-soal
simak ui matematika dasar tahun 2011 kode 212. Pembahasan soal ini tidak sekaligus dalam waktu yang sama. Jadi tetaplah berkunjung ke
blog ini untuk mendapatkan sesuatu yang baru. Semoga dengan pembahasan ini bisa membantu dalam persiapan masuk ui jalur SNMPTN maupun
SIMAK.
1. E (Trigonometri)
Jarak antara titik maksimum dan minimum pada kurva dari fungsi

dengan
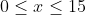
---------------------------------------------------------------------------------
Jawab
---------------------------------------------------------------------------------
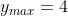
apabila
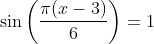

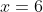
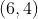
----------------------------------------------------------------------------------
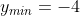
apabila
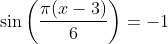
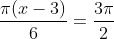
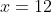
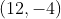
-----------------------------------------------------------------------------------
jarak titik (6,4) dan (12,-4) adalah
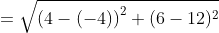
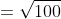
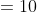
----------------------------------------------------------------------------------
2.C (Suku Banyak)
Diketahui
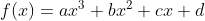
adalah polinomial dengan derajat tiga yang memenuhi persamaan berikut:
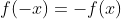
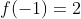
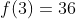
maka
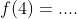
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
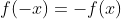
berarti f(x) fungsi ganjil, sehingga
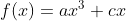
----------------------------------------------------------------------------------
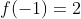
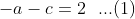
----------------------------------------------------------------------------------
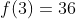
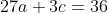
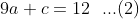
----------------------------------------------------------------------------------
eliminasi persamaan (1) dan (2) diperoleh
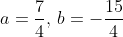
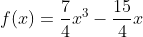
----------------------------------------------------------------------------------
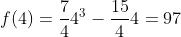
----------------------------------------------------------------------------------
3. A (Fungsi Kuadrat)
Dua titik dengan x
1 = -a dan x2 = 3a dimana a tidak sama dengan nol, terletak pada parabola y = x^2. Garis g menghubungkan kedua titik tersebut. Jika garis singgung parabola di suatu titik sejajar dengan garis g, maka garis singgung tersebut akan memotong sumbu y di ....
----------------------------------------------------------------------------------
Jawab :
----------------------------------------------------------------------------------
perhatikan gambar di atas !
Karena garis g sejajar gris singgung h berarti
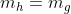
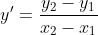
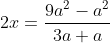
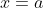
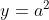
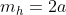
persamaan garis singgung di titik
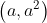
bergradien 2a adalah...
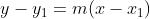
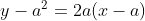
memotong sumbu y berarti x = 0 sehingga diperoleh
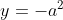
----------------------------------------------------------------------------------
4. C (Peluang)
Huruf-huruf A,H,I,M,O,T,U,V,W,X,Z akan terlihat sama jika dilihat melalui sebuah kaca. Huruf-huruf ini di namakan huruf simetri.
Berapa banyaa cara untuk memilih kata sandi yang terdiri dari 3 huruf dengan paling sedikit 2 huruf simetri?
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
Ada : 26 huruf ( 11 simetri dan 15 tidak)
Ambil : 3 huruf ( paling sedikit 2 huruf simetri)
----------------------------------------------------------------------------------
Ada dua kemungkinan : (asumsikan tidak ada huruf yang sama)
----------------------------------------------------------------------------------
Pertama : 2 simetri 1 tidak
Posisi yang tidak di belakang : 11.10.15 =1650
Posisi yang tidak di depan : 15.11.10 =1650
Posisi yang tidak di tengah : 11.15.10 = 1650
----------------------------------------------------------------------------------
Kedua : 3 simetri
11.10.9 = 990
----------------------------------------------------------------------------------
jumlah seluruhnya 1650.3 + 990 = 5940
----------------------------------------------------------------------------------
5. C (Bilangan Bulat)
Diketahui definisi dari IxI adalah bilangan bulat terbesar yang lebih kecil atau sama dengan x.Sebagai contoh I5I = 5; I2,9I=2; I-2,5I = -3.Jika y adalah bilangan riil yang bukan merupakan bilangan bulat, maka IyI+I2-yI adalah ....
----------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
Perhatikan gambar !

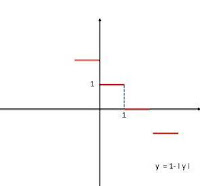
terlihat pada gambar nilai I 2 - y I = 1 - I y I
sehingga I y I + I 2 - y I = I y I + 1 - I y I = 1
-----------------------------------------------------------------
6. A (Trigonometri)
Jika
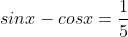
jumlah dari semua nilai tan x yang memenuhi adalah....
---------------------------------------------------------------------------------
Jawab
----------------------------------------------------------------------------------
9.D/E (Sistem Persamaan)
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
Pada suatu segitiga sudut A, B, C berhadapan dengan sisi a, b, c.
maka a = ...































