Pada hari rabu, 05 April 2017 saya di minta tolong untuk konsultasi materi persamaan kuadrat sebagai persiapan menghadapi tes ujian nasional (UN). Ada tujuh siswa yang mau berkonsultasi tentang materi persamaan kuadrat. Karena keterbatasan waktu yang saya punya sehingga saya hanya mengajarkan sub bab pada persamaan kuadrat yang sering muncul pada tes UN yaitu
Menyusun Persamaan Kuadrat
Pada postingan kali ini saya akan menjelaskan materi Menyusun Persamaan Kuadrat dan contoh-contohnya sedangkan materi lengkap persamaan kuadrat bisa di lihat
di SINI
Materi Ringkasnya saya bagi menjadi dua bagian
Bagian 1
Persamaan kuadrat dengan akar-akar p dan q
Langkah - langkahnya
1. Hasil Jumlah Akar (HJA) = p + q
2. Hasil Kali Akar (HKA) = p.q
3. Substitusikan langkah 1 dan 2 ke
Contoh-Contoh
Soal #01
Persamaan kuadrat yang akar-akarnya 3 dan 4 adalah....
Jawab #01
HJA = p + q
HJA = 3 + 4
HJA = 7
HKA = p . q
HKA = 3 . 4
HKA = 12
Soal #02
Persamaan kuadrat yang akar-akarnya -4 dan 2 adalah....
Jawab #02
HJA = p + q
HJA = -4 + 2
HJA = -2
HKA = p . q
HKA = -4 . 2
HKA = -8
Bagian 2
Persamaan kuadrat
dengan akar-akar p dan q, Persamaan kuadrat baru yang akar-akarnya berhubungan dengan akar-akar persamaan kuadrat yang lama
Langkah - langkahnya
1. Menentukan nilai a, b dan c
2. Hasil Jumlah Akar lama (HJAL) = p + q = - b/a
3. Hasil Kali Akar lama (HKAL) = p. q = c/a
4. Hasil Jumlah Akar Baru(HJAB)
5. Hasil Kali Akar Baru (HKAB)
6. Substitusikan langkah 4 dan 5 ke
Contoh-Contoh
Soal #03
Persamaan kuadrat
mempunyai akar-akar p dan q ,
persamaan kuadrat baru yang akar-akarnya p + 5 dan q + 5 adalah....
Jawab #03
a = 1, b = -1, c = 3
HJAL = p + q = -b/a = -(-1)/1 = 1
HKAL= p q = c/a = 3/1 = 3
HJAB = (p + 5) + (q + 5)
HJAB = p + q + 10
HJAB = 1 + 10
HJAB = 11
HKAB = (p + 5)(q + 5)
HKAB = pq + 5p + 5q + 25
HKAB = pq + 5(p + q) + 25
HKAB = 3 + 5.1+ 25
HKAB = 33
Catatan :
Untuk soal no 3 ada cara mudahnya, saya menamakan CARA INVERS,
gimana caranya? Perhatikan pada akar-akar persamaan kuadrat yang baru
yaitu p + 5 dan q + 5 ( kedua akar di tambah dengan nilai yang sama yaitu 5)
Langkah pertama cari invers p + 5
Misalkan
p + 5 = y
p = y - 5
Langkah kedua
Variabel x di persamaan kuadrat lama diganti
dengan ( y - 5) sehingga diperoleh
Soal #04
Persamaan kuadrat
mempunyai akar-akar m dan n ,
persamaan kuadrat baru yang akar-akarnya 2m - 3 dan 2n - 3 adalah....
Jawab #04
a = 1, b = 1, c = - 3
HJAL = m + n = -b/a = -1/1 = - 1
HKAL= m n = c/a = -3/1 = -3
HJAB = (2m - 3) + (2n - 3)
HJAB = 2m + 2n - 6
HJAB = 2(m + n) - 6
HJAB = 2(-1) - 6
HJAB = - 8
HKAB = (2m - 3)(2n - 3)
HKAB = 4mn - 6m - 6n + 9
HKAB = 4mn - 6(m + n) + 9
HKAB = 4.(-3) - 6(-1) + 9
HKAB = -12 + 6 + 9
HKAB = 3
Catatan :
Untuk soal no 4 dapat juga menggunakan CARA INVERS,
gimana caranya? Perhatikan pada akar-akar persamaan kuadrat yang baru
yaitu 2m - 3 dan 2n - 3 ( kedua akar di kuarng 3 lalu dikali 2)
Langkah pertama cari invers 2m - 3
Misalkan
2m - 3 = y
Langkah kedua
Variabel x di persamaan kuadrat lama diganti dengan
Soal #05
Persamaan kuadrat
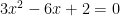
mempunyai akar-akar m dan n ,
persamaan kuadrat baru yang akar-akarnya nnnn
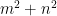
dan 1/m + 1/ n adalah....
Jawab #05
a = 3, b = -6, c = 2
HJAL = m + n = -b/a = -(-6)/3 = 2
HKAL= m n = c/a = 2/3
m^2 + n^2 = (m + n)^2 - 2mn
= (2)^2 - 2.2/3
= 4 - 4/3
= 8/3
1/m + 1/n = (m + n)/mn
= (2)/(2/3)
= 3
HJAB = (m^2 + n^2) + {(m + n)/mn}
HJAB = 8/3 + 3
HJAB = 17/3
HKAB = (m^2 + n^2){(m + n)/mn}
HKAB = 8/3.3
HKAB = 8
x+(HKAB)=0&space;\\&space;\\x^{2}-(17/3)x+(8)=0&space;\\&space;\\3x^{2}-17x+24=0&space;\\ "\\x^{2}-(HJAB)x+(HKAB)=0 \\ \\x^{2}-(17/3)x+(8)=0 \\ \\3x^{2}-17x+24=0 \\")
Jika ada pertanyaan yang ingin ditanyakan, Anda bisa gunakan
live chat yang ada dipojok bawah web ini
Semoga Bermanfaat.
